Author: toosa
Crayon Code Highlighter … and welcome back :)
Sudah lama gak coding akhirnya kembali perlu berenang – renang kembali, ternyata nikmat nya sensasional. Semacam passion yang hilang terus ketemu lagi 🙂 Dan kembali sebagai bayi programmer … meniti satu-persatu wk kkkk
Ops sudah basa-basinya ya … jadi gak nyambung dengan judul di atas he he he
Ok untuk bisa menampilkan code-code saya gunakan plugin di wordpress yang bernama Crayon Code Highlighter. Kenapa Crayon ? karena enak sih 🙂 dan cantik tentunya …
Just try :
<?php echo "Welcome to PHP tutorial"; ?>
Cantik kan tampilan si Crayon … and hey code(s) … welcome back !
Refresh Ubuntu Repository
Sometime whenever you update your Ubuntu (12.x up) and found error message below
Reading package lists… Error!
or like :
W: GPG error: http://archive.ubuntu.com jaunty Release: The following signatures were invalid: BADSIG 40976EAF437D05B5 Ubuntu Archive Automatic Signing Keyetc…
May be your repository configuration in you PC/laptop/server was dirty, and off course you can clean them up using this steps below :
sudo -i apt-get clean cd /var/lib/apt mv lists lists.old mkdir -p lists/partial apt-get clean apt-get update
Hope it will work with You, have a nice try.
Shuffle-Exchange Networks
M.J.Quin pp.59-60
Jaringan Shuffle-Exchange mengandung n = 2k buah node yang ditandai dengan angka 0, 1, … , n-1, dan dua macam koneksi yang disebut shuffle dan exchange. Exchange menghubungkan sepasang nodes yang angkanya berbeda di bit yang terakhirnya. Koneksi?perfect shuffle menghubungkan node i dengan node 2i modulo (n-1), kecuali untuk node yang ke n-1,?dia terhubung dengan dirinya sendiri. Perhatikan gambar 3-8 berikut :
Gambar 3-8
Ini adalah gambar jaringan shuffle-exchange dengan 8 (delapan) buah nodes. Koneksi Shuffle ditandai dengan tanda panah bergaris penuh dan jalur exchange (pertukaran) ditandai dengan panah bergaris putus-putus.
Turunan dari shuffle-exchange salah satunya adalah perfect shuffle. Untuk mendapatkan pemahamam tentang perfect shuffle mari perhatikan ilustrasi berikut ini. Misalkan ada pengocokan kartu sejumlah 8 buah kartu. Mereka ditandai dengan angka 0,1,2,3,4,5,6,7. Jika tumpukan kartu tadi dibagi rata menjadi dua dan kemudian di kocok dengan sempurna, maka hasilnya adalah sebagai berikut : 0,4,1,5,2,6,3,7. Dengan memperhatikan gambar 3-8 di atas, posisi terakhir dari kartu yang dimulai dengan index i dapat ditentukan dengan mengikuti sambungan shuffle dari node i.
Misalkan adalah alamat sebuah node di sebuah jaringan perfect-shuffle dalam bentuk biner. Sebuah data pada alamat ini akan berada di alamat?
sesuai dengan operasi?shuffle. Dengan perkataan lain, perubahan pada alamat dari sebuah data setelah operasi shuffle berkaitan dengan rotasi perputaran kiri (left cylic rotation) dari alamatnya sejauh 1 (satu) bit. Jika n = 2k, maka k kali operasi shuffle memindahkan suatu data kembali ke lokasi asalnya.
The nodes through which a data item beginning at address i travels in response to a sequence of shuffles are called the necklace of i. No necklace is longer than k and a necklace shorter than k is called a short necklace. Figure 3-9 illustrate the necklaces of the perfect shuffle network with eight nodes.
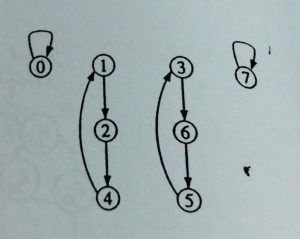
Gambar 3-9
Bitonic Merge
Algoritma ini menjadi dasar untuk algoritma-algoritma sorting dengan waktu proses poli-logaritmik pada beberapa model komputasi paralel. Operasi dasarnya adalah Compare-Exchange: dua buah angka diarahkan masuk ke sebuah Comparator, di dalam comparator ini kedua nilai jika diperlukan akan dipertukarkan, sehingga akan berada pada urutan yang dikehendaki
Definisi 10.1 Bitonic Sequence adalah sederetan nilai \( a_{0}, \cdots ,a_{n-1}\) dengan sifat bahwa
- ada sebuah index i , dimana \( 0\leq i\leq n-1\), sedemikian sehingga a0 menaik secara monoton ke ai dan ai menurun secara monoton hingga an-1 , atau
- ada sebuah pergeseran index yang berputar (cyclic shift) sehingga kondisi yang pertama terpenuhi
Coba Anda perhatikan sebuah grafik barisan bitonic di bawah ini, dia akan memiliki paling banyak ‘satu puncak’ dan ‘satu lembah’. Jangan lupa bahwa barisan ini ‘memutar’ dari elemen yang terakhir kembali ke elemen yang pertama.
Sebuah langkah compare-exchange bisa memecah sebuah barisan bitonic tunggal menjadi 2 (dua) buah barisan bitonic, sebagaimana disebutkan dalam Lemma 10.1 berikut ini :
Lemma 10.1 Jika n adalah genap, maka n/2 buah comparator cukup untuk mentransformasikan sebuah barisan bitonic dengan n buah nilai, \( a_0, a_1, a_2, \cdots , a_{n-2},a_{n-1}\) menjadi 2 (dua) buah barisan bitonic dengan n/2 buah nilai,
\( min(a_0,a_{n/2}), min(a_1,a_{n/2+1}),\cdots ,min(a_{n/2-1},a_{n-1})\)
dan
\( max(a_0,a_{n/2}), max(a_1,a_{n/2+1}),\cdots ,max(a_{n/2-1},a_{n-1})\)Sedemikian sehingga tidak ada nilai yang terletak pada barisan yang pertama adalah lebih besar dari nilai yang terletak pada barisan yang kedua.
Anggaplah kita memiliki sebuah barisan bitonic, sebuah langkah compare-exchange membagi barisan ini menjadi dua buah barisan bitonic yang sama panjang yaitu n/2 . Dengan melakukan langkah ini secara rekursif akan menghasilkan barisan yang terurut.
Atau dengan kata lain, jika diberikan sebuah barisan bitonic dengan panjang n = 2k , dimana k > 0, maka k buah langkah compare-exchange cukup untuk menghasilkan barisan yang terurut
Berikut ini adalah contoh mengurutkan barisan dengan panjang 16 yang di jalankan dalam 4 (empat) langkah compare-exchange.
10-12
Bitonic Merge pada Shuffle-Exchange Nework
Teorema 10.6. Sebuah daftar dengan n = 2k buah elemen yang tidak terurut dan dapat diurutkan dalam waktu dengan jaringan
komparator menggunakan skema interkoneksi shuffle-exchange secara exclusive (Stone, 1971)
Stone menyadari bahwa Pengurut Bitonic milik Batcher ini selalu membandingkan elemen-elemen dengan index yang berbeda tepat 1 bit pada bentuk biner nya. Dengan perfect shuffle, akan memperjalankan elemen pada posisi i ke posisi yang ditemukan., dengan memutar tampilan biner dari i satu bit ke kiri. Dengan demikian dua buah index yang tampilan biner nya berbeda tepat 1 bit dapat diperjalankan ke komparator yang sama dengan cara melakukan sejumlah shuffle tertentu.
Gambar berikut ini menunjukkan bagaimana bitonic merge dapat diimplementasi dengan menggunakan skema interkoneksi shuffle-exchange secara ekslusif.
Sangat berbeda dengan Gambar 10-10, dimana interkoneksi antar komparator nya bervariasi dari tahap ke tahap lainnya. Keseluruhan proses pengurutan dapat diselesaikan dengan menggunakan interkoneksi shuffle-exchange. Kedua algoritma membutuhkan k bitonic merge untuk mengurutkan 2k elemen, tetapi ketika merge ke-i di algoritma Batcher membutuhkan i langkah untuk total k(k+1)/2,
Algoritma
Memasang Eclipse di Ubuntu
Cara memasang Eclipse di Ubuntu (Saya menggunakan Ubuntu 12.10) pada prinsip nya sangat mudah, sama dengan aplikasi-aplikasi lainnya di Ubuntu, caranya : Aktifkan Ubuntu Software Center, lalu pilih Eclipse dan Install. DONE !
Hanya saja versi Eclipse terakhir yang tersedia di repository Ubuntu 12.10 adalah eclipse-platform 3.8.0~rc4-1ubuntu1. Sehingga jika Anda ingin mendapatkan versi terakhir yaitu Juno 4.2.2 SR2, Anda perlu sedikit usaha dengan mendownload dari http://www.eclipse.org/downloads/ lalu pilih yang sesuai dengan platform (OS) yang Anda gunakan.
Saya sarankan kita mulai dari Eclipse yang paling standard yaitu Eclipse Classic 4.2.2, 182 MB. Berhubung file nya cukup besar, jangan lupa siapkan kopi dan snack untuk menikmati penantian downloading nya 🙂
Anda akan mendapatkan file eclipse-SDK-4.2.2-linux-gtk.tar.gz , kemudian extract dengan extract tools yang Anda sukai. Kalau saya lebih memilih menggunakan Nautilus yaitu sebuah File Manager standard dari Gnome yang default terpasang di Ubuntu. Caranya praktis, tinggal klik-kanan, lalu Extract Here, selesai ! 🙂
Tidak ada proses instalasi, tetapi dengan catatan bahwa Java sudah terinstall dengan baik di Ubuntu Anda. Saat tulisan ini dibuat saya menggunakan OpenJDK Java 7 Runtime.
Hasil extract eclipse-SDK-4.2.2-linux-gtk.tar.gz akan menghasilkan sebuah folder Eclipse. Masuklah ke dalamnya lalu jalankan file eclipse yang merupakan executable file. Done !Selanjutkan Anda akan diminta menentukan direktory kerja (workspace) nya ada dimana.
Jika ingin lebih mudah dan nyaman dalam mengaktifkan eclipse, silahkan buat Link di menu, atau diletakkan di Desktop.
Mudah bukan 🙂 Selamat menggunakan eclipse.
Ood-even Transposition Sort Algorithm
Enumeration Sort
Menggabungkan Dua Daftar Terurut
Sebuah Algoritma RAM yang optimal akan membuat satu elemen dalam satu waktu. Algoritma ini memerlukan paling banyak n – 1 buah perbandingan untuk menggabungkan 2 (dua) buah Daftar Terurut yang berukuran n/2. Kompleksitas waktunya . Sedangkan algoritma PRAM hanya membutuhkan
dengan sebuah prosesor untuk setiap elemennya. Dua daftar yang sudah terurut yang akan digabungkan ini memiliki elemen-elemen yang saling disjoint.
(Merging Two Sorted List – Quinn)














