Statistika & Data Sains

Variabel Acak Geometri (Geometric Random Variables)

1 November 2010 toosa Leave a comment

Misalkan ada suatu percobaan yang independent . Setiap kali percobaan itu akan memiliki kemungkinan sukses (probabilitas) sebesar p.

Jika X mewakili banyaknya percobaan awal sebelum akhirnya sebuah sukses terjadi, maka :

$P\left \{ X=n \right \} = p(1-p)^{n-1}, \; n\geq 1$

Sebenarnya rumus di atas dapat mudah dipahami bahwa untuk mendapatkan sukses yang ke-n maka pastilah (n-1) percobaan sebelumnya adalah gagal. Rumus ini berlaku dengan syarat setiap percobaan terjadi secara independent. (percobaan sebelumnya tidak mempengaruhi percobaan berikutnya).

Sebuah Variabel Acak yang memiliki probability mass function seperti di atas disebut Variabel Acak Geometri dengan parameter p.

Mean dari variabel acak geometri ini diperoleh dengan cara sebagai berikut :

$E\left [ X \right ]=\sum_{n-1 }^{\infty} np(1-p)^{n-1}=\frac{1}{p}$

dimana persamaan diatas tersebut menggunakan identitas alajabar untuk 0<x<1,

$\sum_{n=1 }^{\infty} nx^{n-1}=\frac{d}{dx}\left ( \sum_{n=0 }^{\infty} x^{n} \right )=\frac{d}{dx}\left ( \frac{1}{1-x} \right )=\frac{1}{(1-x)^{2}}$

Sehingga dengan demikian tidak lah sulit untuk menghitung variansinya yaitu :

$Var(X)=\frac{1-p}{p^{2}}$

Pemodelan & simulasi, Statistika Elementer Geometric Random Variables, Random Variables, Variabel Acak Geometri

Bilangan Acak

30 September 2010 toosa Leave a comment

Salah satu faktor penting dalam teori simulasi adalah kemampuan untuk membangkitkan bilangan acak. Bilangan acak ini mewakili nilai dari variabel acak yang berdistribusi uniform pada rentang (0,1). Pada bab ini akan dijelaskan bilangan-bilangan acak seperti itu yang dibangkitkan dengan menggunakan komputer dan beberapa ilustrasi penggunaannya.

> Pembangkit Bilangan Acak Pesudo

Pemodelan & simulasi, Statistika & Data Sains, Statistika Elementer

Ruang Sample dan Kejadian

27 September 2010 toosa Leave a comment

Mari kita bayangkan andai ada sebuah percobaan yang kejadian yang mungkin terjadi nya belum kita ketahui pada saat awal.

Semua kejadian yang mungkin terjadi pada percobaan tersebut lalu kita kumpulkan menjadi sebuah kumpulan atau himpunan. Maka kumpulan atau himpunan semacam ini kita sebut dengan Ruang Sample dari suatu percobaan dan biasanya ditandai dengan notasi S.

Contoh, Misalkan ada sebuah balapan kuda yang diikuti oleh 7 ekor kuda. Masing-masing kuda yang diberi nomor punggung 1 hingga 7, maka :

S = { semua urutan dari (1, 2, 3, 4, 5, 6, 7) }

Pemunculan urutan (3,4,1,7,6,5,2) akan berarti bahwa, kuda dengan nomor punggung 3 akan datang paling dulu, baru kemudian disusul oleh kuda nomor 4 dan seterusnya.

Semua himpunan bagian A dari Ruang Sampel disebut sebagai kejadian (event). Karena itu, sebuah kejadian adalah sebuah kumpulan yang mengandung peristiwa yang mungkin muncul dalam suatu percobaan. Jika peristiwa kejadian yang muncul dalam percobaan itu terdapat di dalam A, kita katakan bahwa kejadian A terjadi.

Contoh : A = { semua kejadian di S yang didahului oleh 5 }

Maka A adalah semua peristiwa, dimana kuda nomor 5 yang masuk finish paling dulu.

Untuk sembarang kejadian A dan B, misalkan kita menentukan kejadian baru $A\cup B$ , yang disebut juga union/gabungan A dan B, gabungan ini mengandung semua kejadian yang mungkin muncul yang mungkin saja berada di dalam A atau di dalam B atau berada dikeduanya A dan B. Sejalan dengan hal tersebut, kita tentukan kejadian, AB, yang disebut sebagai irisan/ intersection dari A dan B, dimana kejadian AB terjadi jika A dan B juga terjadi. Kita juga bisa menentukan gabungan dan irisan untuk lebih dari 2(dua) kejadian. Gabungan dari kejadian-kejadian $A_1, \cdots , A_n$ ditulis $\bigcup_{i=1}^{n} = A_i$ ditentukan memuat semua kejadian yang berada di sembarang $A_i$. Begitu pula dengan irisan dari kejadian-kejadian $A_1, \cdots , A_n$ ditulis dengan $A_1A_2 \cdots A_n$ yang mengandung semua kejadian yang mungkin muncul (outcome) berada di semua $A_i$.

Untuk semua kejadian A ada kejadian yang disebut $A^c$ , sering disebut sebagai komplemen dari A. mengandung semua kejadian di ruang sample S tapi tidak berada di A. Karena itu, $A^c$ terjadi jika dan hanya jika A tidak terjadi. Karena kejadian yang mungkin muncul haruslah berada di ruang sample S, akibatnya $S^c$ tidak mengandung kejadian apapun, karenanya tidak muncul apapun. Kita sebut $S^c$ himpunan null dan ditulis dengan 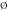$\small \inline \o$ . Jika 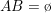$\small \inline AB =\o$ , dikatakan bahwa A dan B mutualy exclusive

Pemodelan & simulasi, Statistika Elementer Kejadian, Ruang Sample

Variabel Acak

18 December 2009 toosa Leave a comment

Ketika sebuah percobaan dilakukan, biasanya hasil kejadian yang diperoleh berupa ‘nama kejadian’ seperti : buka dan tutup; terang, redup dan gelap; merah, kuning dan hijau; hidup dan mati dan lain sebagainya. Informasi kejadian yang berbentuk seperti demikian itu belum dapat kita gunakan dalam perhitungan matematis.

Oleh karenanya agar kita bisa olah lebih lanjut, kita harus mengubahnya menjadi suatu bentuk kuantitatif berupa nilai numerik yang menjelaskan hasil percobaan/kejadian tersebut. Nilai kuantitatif yang menjelaskan hasil percobaan/kejadian ini dikenal dengan istilah variabel acak (random variables).

Misalkan ada sebuah percobaan yang memiliki outcome (semua kejadian yang mungkin muncul dalam percobaan) berupa benar dan salah. Maka ketika benar diwakilkan dengan angka 1 dan salah diwakilkan dengan angka 0, maka 0 dan 1 adalah numerik yang mewakili kejadian random benar dan salah yang pada akhirnya disebut sebagai variabel acak. Jadi boleh dikatakan bahwa variabel acak adalah sebuah fungsi yang memetakan kejadian yang ada di alam menjadi bilangan numerik. Semua kejadian yang mungkin muncul dalam suatu percobaan kita sebut sebagai anggota Ruang Sample yang dinotasikan dengan S.

Contoh :

Lemparlah sebuah uang logam yang memiliki sisi atas (kejadian muncul sisi atas kita sebut A), dan sisi bawah (kejadian muncul sisi atas kita sebut B) sebanyak 10 kali. Maka :

Ruang sample perobaan ini adalah S = {AABBABABAB, … } meliputi semua konfigurasi dari A dan B.
Misalkan Variabel Acak X adalah banyaknya nya Sisi Atas yang muncul, $X:S \to \Re $ atau dalam contoh ini $X:S \to \left \{ 0,1, \cdots,10 \right \} $

Fungsi distribusi kumulatif atau biasanya disingkat fungsi distribusi saja, F dari variabel acak X untuk sembarang bilangan riil x ditentukan dengan :

$F(x)= P\left \{ X\leq x \right \}$

Sebuah Variabel Acak disebut diskrit jika variabel acak ini terdiri dari sejumlah angka yang terhitung dan terbatas dari nilai-nilai yang mungkin terjadi. Untuk sebuah variabel acak diskrit X kita tentukan Fungsi Masa Probabilitas (Probability Mass Function) p(x) dengan :

$p(x)= P\left \{ X= x \right \}$

Jika X adalah variabel acak diskrit yang memiliki nilai yang mungkin muncul $ x_1, x_2,\cdots$, maka karena X harus berasal dari salah satu nilai-nilai tersebut, kita akan memperoleh :

$\sum_{i=1}^{\infty }p(x_i)=1$

Contoh : Misalkan X bernilai dari salah satu 1,2 atau 3. Jika

$p(1)=\frac{1}{4},\; \; \; p(2)=\frac{1}{3} $

maka, karena $p(1)+p(2)+p(3)=1$ , akan menghasilkan $p(3)=\frac{5}{12}$

Pemodelan & simulasi, Statistika Elementer Variabel Acak