toosa – Page 9 – OpenStat

Memfungsikan PHP di userdir Apache Ubuntu 10.10

7 August 2011 toosa Leave a comment

Ketika apache dan php di install di Linux Ubuntu 10.10, php memang sudah bisa dijalankan di /var/www, tetapi ketika kita mengaktifkan modul userdir agar /home/username/public_html bisa digunakan, ternyata baru .html yang bisa diaktifkan, sedangkan *.php belum bisa berjalan. ini karena secara default php5.conf belum mengaktifkan php di public_html.

Bukalah file /etc/apache2/mods-enabled/php5.conf :

<IfModule mod_php5.c>
    <FilesMatch "\.ph(p3?|tml)$">
        SetHandler application/x-httpd-php
    </FilesMatch>
    <FilesMatch "\.phps$">
        SetHandler application/x-httpd-php-source
    </FilesMatch>
    # To re-enable php in user directories comment the following lines
    # (from <IfModule …> to </IfModule>.) Do NOT set it to On as it
    # prevents .htaccess files from disabling it.
    <IfModule mod_userdir.c>
         <Directory /home/*/public_html>
             php_admin_value engine Off
         </Directory>
    </IfModule>
</IfModule>

Anda harus memberikan remark (#) seperti di bawah ini :

<IfModule mod_php5.c>
    <FilesMatch "\.ph(p3?|tml)$">
        SetHandler application/x-httpd-php
    </FilesMatch>
    <FilesMatch "\.phps$">
        SetHandler application/x-httpd-php-source
    </FilesMatch>
    # To re-enable php in user directories comment the following lines
    # (from <IfModule …> to </IfModule>.) Do NOT set it to On as it
    # prevents .htaccess files from disabling it.
   # <IfModule mod_userdir.c>
   #     <Directory /home/*/public_html>
   #          php_admin_value engine Off
   #     </Directory>
   # </IfModule>
</IfModule>

Terakhir jangan lupa merestart Apache nya :

$ /etc.init.d/apache2 restart

Apache, PHP, Ubuntu, Web Tech

Start Using Zend Framework 1.11

17 July 2011 toosa Leave a comment

Zend Framework is one of popular PHP Framework which mostly use for enterprise application. So it will be a little bit complex for the beginers. But don’t worry, I am a beginers too :). I assume that your server is the same with mine, it use linux/unix operating system and can be accessed by ssh/telnet. When I wrote this post, I still use ZF ver. 1.11.

Ok then, lets rock !

1. Get Zend Framework and prepare your site based on Zend Framework

We will get the latest zend framework ini minimal configuration , extract and rename it (I choose ZendFramework-1.11.9-minimal) to ZendFramework then place it under public_html directory (or you can place as you like).

# cd /home/username/public_html

# tar -zxvf ZendFramework-1.11.9-minimal.tar.gz

# mv ZendFramework-1.11.9-minimal ZendFramework

We will use Zend Tools which located in ZendFramework/bin/zf.sh, so we need to create an alias. You need to modify /home/username/.bashrc by add the text bellow at the end of file :

alias zf.sh=/home/username/public_html/ZendFramework/bin/zf.sh

After you modify this file, you need to re-login. Now, every time You login, Zend tools is ready to use 🙂

Check your Zend Tools :

# zf.sh show version

Zend Framework Version: 1.11.9

2. Create a ZF project (let say “zfstart”).

# cd /home/username/public_html

# zf.sh create project zfstart

3. Create a symbolic link of your zend library to your project library directory

# cd /home/username/public_html/zfstart/library

# ln -s /home/username/public_html/ZendFramework/library/Zend

4. And finaly you will have zfstart project directory structure bellow:

5. Test your project

http://yourdomain/zfstart/public

Then you should see like this bellow :

Congratulation !

Zend Framework (ZF1)

Masalah Perbaikan (Repair Problem)

4 June 2011 toosa Leave a comment

Misalkan ada sebuah sistem yang membutuhkan tepat n buah mesin, dan tidak boleh kurang dari n. Jika kurang maka system ini tidak dapat berfungsi alias gagal.

Untuk menjaga agar sistem ini dapat terus beroperasi dengan baik, maka disediakanlah mesin cadangan. Ketika ada sebuah mesin yang rusak, maka seketika itu pula mesin cadangan langsung digunakan, dan mesin yang rusak tadi langsung dibawa ke bengkel perbaikan mesin. Bengkel tersebut hanya bisa memperbaiki 1 (satu) buah mesin dalam satu waktu, selebihnya harus antri untuk diperbaiki kemudian. (Lihat gambar)

Semua lamanya waktu perbaikan adalah variabel random independent dengan distribusi G (Gamma). Setiap kali mesin digunakan, maka waktu yang dihabiskan sampai akhirnya mesin tersebut rusak adalah variabel random dan independent berdistribusi F (poisson).

Sistem ini dikatakan gagal apabila terjadi kondisi sebuah mesin rusak dan tidak ada mesin cadangan yang tersedia untuk menggantikannya.

Asumsikan bahwa pada awalnya terdapat n + s mesin yang berfungsi dengan baik, n buah yang beroperasi dan s buah sebagai cadangan, kita akan mensimulasikan sistem ini, demikian juga sebagai pendekatan E[T], dimana T adalah waktu ketika sistem nya gagal operasional.

Untuk mensimulasikan hal ini, kita akan menggunakan variabel berikut :

Variabel waktu : t
Variabel Status Sistem : r ( banyaknya mesin yang rusak pada waktu t)

Variabel Status sistem dapat berubah kapanpun, baik karena sebuah mesin yang sedang bekerja saat itu menjadi rusak, atau ketika suatu mesin yang rusak ternyata sudah selesai diperbaiki, dengan kata lain dikatakan bahwa sebuah kejadian terjadi ketika salah satu atau kedua persistiwa ini terjadi.

Untuk mengetahui kapan kejadian berikutnya akan terjadi, kita perlu terus mengikuti saat-saat ketika mesin yang sedang beroperasi menjadi rusak dan suatu saat ketika suatu mesin yang sedang diperbaiki ternyata sudah selesai dan siap beroperasi kembali.

Kita membutuhkan informasi tersebut untuk menentukan waktu terkecil dari n buah waktu kejadian mesin rusak, simpan informasi ini dalam sebuah daftar terurut.

Daftar kejadian : $ t_1\leq t_2\leq t_3 \leq …\leq t_n ,t^* $

Dimana t₁ , … , t_n adalah waktu (berurutan) dimana n buah mesin yang sekarang sedang beroperasi akan rusak, dan t^* adalah waktu dimana mesin yang saat itu sedang diperbaiki akan selesai diperbaiki dan siap beoperasi lagi, jika tidak ada mesin yang sedang di perbaiki maka t^* = $ \infty $

Mari sekarang kita lakukan simulasinya :

Inisialisasi

Tentukan $t=r=0, t^{*}=\infty $ ,

Bangkitkan $ X_1, … , X_n $ variabel independent yang memiliki distribusi F. Urutkan nilai-nilai ini dan $ t_i $ adalah nilai terkecil yang ke-i, i = 1, … , n.

Buat daftar kejadian : $ t_1, . . . , t_n , t^*$

Selanjutnya kita akan berhadapan dengan dua kasus berikut :

Case 1 $ t_1 < t^*$

Atur kembali : $ t = t_1$.

Atur : r = r + 1 (karena mesin yang lain ada yang rusak)

Jika r = s + 1, hentikan proses ini dan ambil data dari T = t ( ketika ada s + 1 mesin rusak, dan tidak ada cadangan)

Jika r < s + 1, bangkitkan variabel random X yang berdistribusi F. Variabel random ini akan menampilkan waktu kerja dari bengkel perbaikan yang akan digunakan kembali saat ini. Sekarang urutkan kembali nilai-nilai $ t_2,t_3,\cdots, t_n , t + X $ dan jadikan $ t_i $ sebagai nilai terkecil ke-i dari nilai-nilai tersebut, dimana i = 1, … , n.

Jika r = 1, bangkitkan variabel random Y yang mempunyai fungsi distribusi G dan atur t^* = t + Y (hal ini diperlukan karena dalam kondisi ketika sebuah baru saja rusak adalah satu-satunya mesin yang beroperasi, dan dengan demikian perbaikan agak segera dilakukan padanya. Y akan menjadi lamanya waktu perbaikan dan karenanya perbaikan akan selesai pada saat t + Y).

Case 2 $ t^* \leq t_1$

Atur: t = t^*

Atur: r = r – 1

Jika r > 0, bangkitkan variabel random Y yang memiliki fungsi distribusi G, dan tampilkan kembali lamanya waktu perbaikan dari mesin yang baru saja masuk ke bengkel perbaikan, dan atur $ t^* = t + Y$

Jika r = 0, atur $ t^* = \infty $.

Aturan di atas diilustrasikan pada gambar berikut :

Setiap kali kita berhenti (yaitu pada saat r = s + 1), kita katakan bahwa sebuah operasi selesai dilakukan. Output dari operasional ini adalah nilai dari waktu gagal operasional T. Kita nanti kemudian akan memulai lagi dari awal dan mensimulasikan operasional berikutnya. Secara keseluruhan, misalkan kita melakukan k kali operasional dengan ouput masing-masing $ t_1, T_2, … , T_k $, karena semua k variabel random adalah independent dan setiapnya mewakili waktu kegagalan sistem, rata-ratanya $ \sum_{i=1}^{k}T_i/k $ adalam estimasi dari E[T], mean dari waktu kegagalan sistem.

Pemodelan & simulasi Repair Problem

Perkalian Matrik pada Mesh

23 May 2011 toosa Leave a comment

Asumsikan bahwa kita akan mengalikan dua matrik A dan B yang berukuran n x n pada komputer SIMD Mesh Connected dengan n² prosesor.

1. Batas bawah untuk Perkalian Matrik pada Mesh

Asumsi :

(A1) Setiap anggota matrik yang akan diperkalikan hanya diwakilkan hanya satu kali pada model komputasi

(A2) Tidak ada 2 (dua) anggota matrik yang sama disimpan pada prosesor yang sama

Teorema :

Berdasarkan asumsi A1 dan A2 di atas, dan tanpa menggunakan sembarang fasilitas broadcast, perkalian dari dua matrik A dan B yang berukuran n x n yang akan menghasilkan C yang juga berukuran n x n, paling tidak akan membutuhkan d langkah pergerakan data, dimana $ \beta (2d) \geq n^2 $

2. Perkalian Matrik pada Mesh dengan Koneksi Berkeliling (Wraparound)

Komputer Mesh Connected dengan Koneksi Berkeliling bisa digambarkan seperti gambar berikut :

Asumsi bahwa matrik yang akan diperkalikan berukuran n x n dan banyaknya prosesor di Mesh adalah n² . p_ijadalah prosesor pada baris ke i dan kolom ke j, dan terhubung dengan prosesor p_(i-1)j, p_i(j+1), p_(i+1)j, dan p_i(j-1), jika ada. Sebagai tambahan, diasumsikan bahwa pada bagian batas-batas tepian dari Mesh saling terhubung. Keterhubungan keliling ini menjadikan semua proses penjumlahan dan pengurangan menggunakan modulo n.

Algoritma MESH_MATRIX_MULT1

Input : anggota-2 A[i,j] dan B{i,j] dari matrik A dan B tersedia di prosesor p_ij, $ 0 \leq i, j \leq n – 1 $

Ouput : Elemen C[i,j] dari produk matrix tersedia di prosesor p_ij , $ 0 \leq i, j \leq n – 1 $

for i =1 to n – 1 dopar

for s = 1 to i do

for j = 0 to n -1 dopar

A[i,j] := A[i, {j+1) mod n]

odpar

od

odpar

forj = 1 to n – 1 dopar

for t = 1 to j do

for i = 0 to n -1 dopar

B[i,j] := B[(i+1) mod n, j]

odpar

od

odpar

for i = 0 to n – 1 dopar

for j = 0 to n – 1 dopar

C[i,j] := A[i,j] x B[i,j]

odpar

odpar

for k = 0 to n – 1 do

for i = 0 to n – 1 dopar

for j = 0 to n – 1 dopar

A[i,j] := A[i, (j+1) mod n]

B[i,j] := B[(i+1) mod n, j]

C[i,j] := A[i,j] x B[i,j]

odpar

odpar

od

Analisa Kompleksitas

Tampak jelas bahwai perulangan for paralel pertama membutuhkan tidak lebih dari O(n) waktu.

Kita bisa melakukan pergeseran baris (row-shifting) dalam n/2 langkah paralel dengan cara menggeser elemen tersebut ke kanan ketika angka perpindahan lebih besar dari n/2.

Begitupun, paralel kedua statemen for perpindahan kolomnya membutuhkan O(n) waktu. Kita belum memulai operasi aritmatika. Operasi aritmatika ditampilkan pada perulangan for yang ketiga dan keempat. Perulangan for yang ketiga secara nyata membutuhkan O(1) waktu paralel. Terakhir, perulangan for yang keempat membutuhkan O(n) waktu sejak badan dari perulangan for ini terdiri dari dua perulangan for paralel bersarang bisa diimplementasikan pada O(1) waktu. Karena itu, waktu keseluruhan kompleksitas algoritma MESH_MATRIX_MULTI adalah O(n) pada sebuah mesh dengan n² prosesor. Dengan jelas, algoritma ini optimal untuk melihat ?(n) untuk bound yang lebih rendah pada waktu komputasi untuk perkalian matrik pada mesh dua dimensi. Nilai dari algoritma adalah O(n³) yang seperti algoritma straightforward serial matrix multiplication.

…

3. Perkalian Matrik pada Mesh tanpa Koneksi Berkeliling (Wraparound)

Pada bagian ini, kita membahas algoritma perkalian matrik pada mesh dua dimensi yang terhubung dengan komputer tanpa koneksi wraparound. Pada model ini prosesor dihubungkan denga keempat yang terdekat kecuali prosesor yang ada di perbatasan yang juga terhubung dengan keduanya (Kasus : permasalahan disudut- sudut prosesor), atau ketiganya (perbatasan disetiap empat sudut prosesor).

Kita mengasumsikan bahwa algoritma dari elemen A dan B dikirim ke batas prosesor di dalam baris dan kolom pertama dari permasalahan masing- masing. Elemen- elemen dari matriks dikirimkan melalui baris 1 dari A setelah baris i-1, untuk 1 ? j ? n-1. Begitupun kolom j dari B dilaksanakan setelah kolom j-1, untuk 1 ? j ? n-1. ini menjelaskan dari gambar 6.3a untuk kasus- kasus matriks 2 x 2. tiap prosesor pij diatas menerima A[i,k] dan B[k,j, untuk 0 ? k ? n-1, melipatgandakan dan menambahkan hasil ke bagian hasil C[i,j] (C[i,j] menginisialkan ke 0 dari semula). Akhirnya, p_ij mengirim A[i,k] ke p_i(j+1) jika 1 < n-1 dan B[k,j] ke p_(i+1)j jika i < n-1. proses ini terus berulang hingga produk matriks C = A x B terpenuhi sebagai output. Algoritma paralel berdasarkan ide diatas seperti dibawah ini.

Algoritma MESH_MATRIX_MULT2

Input: elemen- elemen A[i,j] dan B[i,j,i] = 0,1,…,n-1 dari A dan B dikirimkan ke prosesor dari kolom paling kiri (j=0) dan baris paling atas (i-0), masing- masing.

Ouput: matriks C = A x B disimpan jadi elemen- elemen C[i,j] tersedia diprosesor p_ij,i,j = 0,1,…,n-1

For i = 0 to n-1 dopar

For j = 0 to n-1 dopar

C[i,j] := 0

Odpar

Odpar

For i = 0 to n-1

For j = 0 to n-1 dopar

While (p_ij receives A[i,k] and B[k,j], k ? (0,1,…,n-1) do

C[i,j] := C[i,j] + A[i,k] x B[k,j]

If i<n-1

Then send B[k,j] to p_(i+1)j

Fi

If j < n-1

Then send A[i,k] to p_i(j+1)

Fi

Od

Odpar

Odpar

Paralel Algorithm Mesh, Perkalian Matrik

Simulasi dengan perantara Kejadian Diskrit

19 May 2011 toosa Leave a comment

Elemen kunci dari simulasi kejadian diskrit adalah variabel-variabel dan kejadian-kejadian. Untuk melakukan simulasi kita secara kontinyu mengamati beberapa variabel tertentu. Secara umum, ada tiga jenis variabel yang sering digunakan,?variabel waktu, variabel penghitung (counter),dan?variabel status sistem (system state).

Variabel

	Varible	Description
1.	Time : t	Amount of (simulated) time that has elapsed
2.	Counter	Keep a count of the number of times that certain events have occurred by time t
3.	System State	Describe the "state of the system" at the time t

Ketika sebuah kejadian muncul, nilai dari variabel-variabel di atas akan berubah atau diperbaharui, dan kita akan mengambilnya sebagai keluaran untuk suatu data pengamatan. Untuk tujuan menentukan kapan kejadian berikutnya akan muncul, kita akan memelihara sebuah “daftar kejadian”, yang akan berisi daftar kejadian masa depan terdekat yang akan terjadi dan kapan kejadian tersebut dijadwalkan akan terjadi.

Ketika sebuah peristiwa terjadi, kita akan mengatur kembali waktu dan semua status serta variabel penghitung, serta mengambil data yang terkait. Dengan cara ini , kita akan dapat menelusuri/mengikuti sistem selama sistem itu berproses sepanjang waktu tertentu.

Dalam semua model antrian, kita mengambil anggapan bahwa para pelanggan akan datang mengikuti suatu proses poisson nonhomogeneous dengan fungsi intensitas terbatas?$\lambda (t), t > 0$. Ketika mensimulasikan model ini, kita akan menggunakan subrutin berikut ini untuk membangkitkan nilai dari variabel acak $ T_s $, ditentukan sama waktunya dengan kedatangan pertama kalinya setelah?s?satuan waktu berlalu.

Misalkan $\lambda $ sedemikian sehingga $\lambda (t)\leq \lambda $ untuk semua?t. Asumsikan bahwa?$\lambda (t), t > 0$, dan ?$\lambda $ sudah ditentukan, subrutin berikut ini akan membangkitkan nilai dari?$ T_s $.

Subrutin untuk membangkitkan Ts

[table “2” not found /]

Pemodelan & simulasi Kejadian Diskrit

Paralel Algorithm Design and Analysis: Sebuah Urutan Pembelajaran

14 May 2011 toosa Leave a comment

Sebuah usulan urutan pembelajaran Algoritma Dan Pemrosesan Paralel

Pengenalan dan latar belakang
Terminologi Komputer Paralel
Models dan Paradigma Komputer Paralel
Processor Arrays, Multiprocessors, dan Multicomputers
1. Organisasi Processor
  1. Cube Connected Cycles Networks
  2. Shuffle-Exchange Networks
Analisa Kompleksitas Algoritma Paralel
Algoritma-algoritma PRAM
1. Parallel Reduction
2. Prefix Sums
3. List Ranking
4. Preorder Tree Traversal
5. Merging Two Sorted Lists
6. Graph Coloring
Sorting
1. Enumeration Sort
2. Lower Bounds On Parallel Sorting
3. Ood-even Transposition Sort Algorithm
4. Bitonic Merge
5. Bitonic Merge pada Shuffle-Exchange Nework
Selection dan Searching
Komputasi Matriks
1. Pengantar Komputasi Matrik
2. Perkalian Matrik secara umum
Algoritma untuk Grap Tak Berbobot
Algoritma untuk Grap Berbobot

Paralel Algorithm Urutan Pembelajaran

Pendekatan Simulasi Kejadian Diskrit (The Discrete Event Simulation Approach)

13 May 2011 toosa Leave a comment

Mensimulasikan suatu model probabilistik akan melibatkan pembangkitan mekanisme stokastik dari model yang bersangkutan dan kemudian melakukan pengamatan terhadap aliran resultante dari model tersebut sepanjang waktu tertentu.

Berdasarkan kepada alasan pembuatan simulasi tersebut, akan ada beberapa kuantitas pengamatan tertentu yang akan kita cari. Tetapi , walaupun demikian karena evolusi model yang mengikuti waktu itu sering kali melibatkan suatu struktur logis yang rumit dari elemen-elemennya, karenanya tidak selalu mudah untuk melakukan penelusuran/mengikuti perjalanan dari evolusi tersebut, demikian juga dalam menentukan kuantitas yang akan diamati.

Sebuah kerangka kerja (framework) umum, dibangun seputar ide dari “kejadian diskrit”, telah dibuat untuk membantu kita untuk mengikuti sebuah model sepanjang waktu dan menentukan kuantitas pengamatan yang relevan/wajar. Pendekatan pada simulasi yang berdasarkan pada kerangka kerja ini sering disebut dengan Pendekatan Simulasi Kejadian Diskrit.

Pemodelan & simulasi Pemodelan & Simulasi

Sistem Antrian dengan 2 (dua) Server Paralel

13 May 2011 toosa Leave a comment

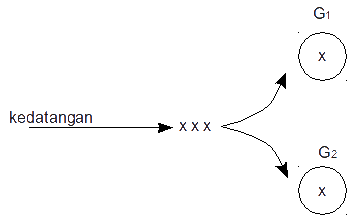
Sistem ini terdiri dari 2 (dua) server, dimana ketika pelanggan datang pada saat kedua server dalam keadaan sibuk, maka pelanggan tersebut akan masuk dalam antrian. Dan ketika salah satu server kosong/bebas, maka segera pelanggan yang datang lebih dahulu dalam antrian akan masuk ke dalam server yang kosong/bebas itu, tidak tergantung server nomor berapa yang sedang kosong. Distribusi layanan dari server ke i adalah $ G_i $, i=1,2 (lihat gambar)

Misalkan kita akan mensimulasikan model ini, sambil mengamati waktu yang dihabiskan oleh setiap pelanggan didalam sistem dan banyaknya layanan yang diberikan/dilakukan oleh setiap server.

Karena disini kita memiliki lebih dari satu server, maka akan berdampak bahwa nanti ketika pelanggan meninggalkan sistem, urutannya mungkin tidak sama dengan urutan ketika dia datang. Karenanya untuk mengetahui pelanggan mana yang akan meninggalkan sistem pada saat layanannya selesai kita akan mencermati pelanggan mana saja yang sedang dalam sistem.

Kita akan memberi nomor pada setiap pelanggan yang baru saja sampai di sistem, yang pertama kali datang diberi nomor 1, berikutnya 2, dan selanjutnya. Kita akan menggunakan variabel-variabel berikut :

Variabel waktu t

System State Variable (SS)

Variabel yang mencatat kondisi sistem (System State) pada waktu tertentu.

( $ n, i_1, i_2, . . ., i_n $ ) jika ada n pelanggan di dalam sistem $i_1$ akan bersama dengan server 1, $i_2 $ akan bersama dengan server 2, $ i_3 $ akan bersama dengan server 3 dan seterusnya.

Catatan : SS = (0) ketika sistem kosong/bebas, dan SS = (1,j,0) atau (1,0,j) ketika hanya pelanggan j dan dia sedang dilayani di server 1 atau server 2.

Counter Variables (variabel penghitung)

$ N_A $ : banyaknya kedatangan dalam waktu t .

$ C_j $ : banyaknya pelanggan yang dilayani oleh j, j= 1,2, dalam waktu t .

Output Variables

Variabel yang mencatat kejadian apa saja dan berapa yang dihasilkan dari sistem.

A(n) : waktu kedatangan dari pelanggan n, $ n \geq 1$

D(n) : waktu keberangkatan pelanggan n, $ n \geq 1$

Event list $ t_A , t_1 , t_2$

Dimana $ t_A $ adalah waktu kedatangan berikutnya, dan $ t_1 $ adalah waktu penyelesaian dari pelanggan yang pada saat itu sedang dilayani oleh server i, i = 1, 2. Jika tidak ada lagi pelanggan yang saat itu berada di server i, maka kita jadikan $ t_i = \infty $, i = 1, 2. Berikut ini, daftar kejadian akan selalu berisi tiga variabel yaitu $ t_A , t_1 , t_2 $.

Untuk memulai simulasi, kita berikan nilai awal pada variabel-variabel dan daftar kejadian tersebut sebagian berikut :

Pemberian nilai awal (Initialize)

Set t = $ t_A = C_1 = C_2 = 0$

Set SS = (0)

Bangkitkan $ T_0$, dan set $ t_A = T_0, T_1 = t_2 =\infty $.

Untuk mengupdate sistem. kita bergerak dalam waktu tertentu hingga kita mencapai event/kejadian berikutnya. Pada kasus-kasus berikut, $Y_i $ selalu berasal dari variabel acak yang berdistribusi $ G_i , i=1,2$

Kasus 1 $ SS = (n, i_1, i_2, … , i_n) $ dan $ t_A = min (t_A, t_1, t_2 )$

Reset : $ t = t_A$

Reset : $ N_A = N_A + 1$

Bangkitkan $ T_t $ dan reset $ t_A = T_t$

Ambil output data $ A(N_A) = t$

Jika SS = (0):

Reset : $SS = (1, N_A,0)$

Bangkitkan $ Y_1 $ dan reset $ t_1 = t + Y_1$

Jika SS = (1, j, 0) :

Reset : $ SS = (2, j, N_A)$

Bangkitkan $Y_2 $ dan reset $t_2$

[ Sumber : Simulation, Sheldon M. Ross]

Pemodelan & simulasi Simulasi Diskrit, Sistem Antrian

Penggabungan/Merging pada model CREW PRAM

17 April 2011 toosa Leave a comment

Sumber : Parallel Algorithms, Design and Analysis by Pranay Chaudhuri

Algoritma ini ditujukan untuk menggabungkan dua buah list yang panjangnya sama, n., dan jumlah prosesor yang digunakan juga n buah.

Algoritma MERGE1_CREW

Input : Dua buah list terurut

p { margin-bottom: 0.21cm; }

Input : Dua buah list terurut yaitu X={ x₁, x₂, … ,x_n} dan Y={ y₁, y₂, … ,y_n}

Ouput : List terurut Z={ z₁, z₂, … , z_2n} yang merupakan hasil penggabungan dari X dan Y

for i = 1 to n dopar

temukan y_j yang paling kecil sedemikian sehingga (such that) x_i < y_j

if y_j ditemukan (exists)

then z_{i+j -1} :=x_i

else z_n+i :=x_i

fi

temukan x_j yang paling kecil sedemikian sehingga (such that) y_i < x_j

if x_j ditemukan (exists)

then z_{i+j -1} :=y_i

else z_n+i :=y_i

fi

odpar

Semua n prosesor mengeksekusi 4 langkah di dalam loop pada algoritma MERGE1_CREW secara paralel.

Untuk menemukan y_jyang paling kecil sedemikian sehingga x_i < y_j dan x_j yang paling kecil sedemikian sehingga y_i < x_j kita bisa menggunakan algoritma serial binary search. Binary Search ini membutuhkan waktu O(log n) pada single prosesor untuk setiap i. Sedang untuk proses yang lainnya hanya membutuhkan waktu O(1) saja. Karena itu secara keseluruhan kompleksitas dari algoritma ini adalah O(log n) dengan menggunakan n buah prosesor.

Walaupun algoritma ini cukup sederhana dan mudah dimengerti tapi :

hanya berlaku jika kedua list terurut yang akan digabungkan memiliki panjang yang sama
hanya berlaku jika tidak ada elemen yang sama yang muncul antara X dan Y, jika terdapat yang sama maka algoritma ini bisa digunakan dengan asumsi bahwa elemen yang sama di X dianggap lebih kecil dari elemen yang sama di Y
secara cost masih sangat mahal, yaitu O(n log n)

Selanjutnya akan dikenalkan algoritma lain yang lebih umum, yang tidak mengharuskan ukuran List Terurut nya sama, jumlah prosesor pun dapat dibatasi sesuai dengan ketersediaan/kebutuhan. Algoritma ini bernama Algorithm MERGE2_CREW.

p { margin-bottom: 0.21cm; }

Input : Dua buah list terurut yaitu X={ x₁, x₂, … ,x_m} dan Y={ y₁, y₂, … ,y_n}, dimana m ?n

Ouput : List terurut Z={ z₁, z₂, … , z_m+n} yang merupakan hasil penggabungan dari X dan Y

for i = 1 to P-1 dopar

/* Setiap prosesor i akan menemukan x_isdan y_is dari list X dan Y secara berurutan sehingga membentuk list X_s={ x_1s, x_2s, … ,x_(P-1)s} dan Y_s={ y_1s, y_2s, … ,y_(P-1)s} */

x_1s = x_i_?_m/P_?;

y_1s = y_i_?_n/P_?;

odpar

for i = 1 to P-1 dopar

/* Langkah berikut ini akan membentuk list L yang panjangnya 2P-2. L dihasilkan dalam bentuk array (2P-2) x 3, dimana setiap k ( 1 ? k ? 2P-2), L(k,1) memuat nilai dari elemen ke-k dalam gabungan dari X_sdan Y_s ; L(k,2) memuat index dari posisi aslinya di dalam X_satau Y_s; dan L(k,3) mencatat dari mana X atau Y yang menjadi sumber dari nilai tersebut) */

Temukan j yang paling kecil sedemikian sehingga x_is < y_js;

If y_js exists/ada

Then do

L(i+j-1,1) := x_is ;

L(i+j-1,2) := i ;

L(i+j-1,3) := X ;

else do

L(i+P-1,1) := x_is ;

L(i+P-1,2) := i ;

L(i+P-1,3) := X ;

Temukan j yang paling kecil sedemikian sehingga y_is < x_js;

If x_js exists/ada

Then do

L(i+j-1,1) := y_is ;

L(i+j-1,2) := i ;

L(i+j-1,3) := Y ;

else do

L(i+P-1,1) := y_is ;

L(i+P-1,2) := i ;

L(i+P-1,3) := Y ;

odpar

for i = 1 to P dopar

/* Setiap prosesor i akan menemukan titik awalnya BX(i) dan BY(i) untuk penggabungan dua sublist dari X dan Y, dengan kata lain prosesor i akan bertanggung jawab terhadap penggabungan sublists yang diawali dengan x_BX(i) dan y_BX(i)di dalam X dan Y, secara berurutan */

if i = 1

then do

BX(1) := 1;

BY(1) := 1

else if L(2i – 2,3) = X

then do

Temukan j yang paling kecil sedemikian sehingga L(2i – 2,1) < y_j;

BX(i) := L(2i – 2,1) ? m/P? ;

BY(i) := j

else do

Temukan j yang paling kecil sedemikian sehingga L(2i – 2,1) < x_j;

BX(i) := j;

BY(i) := L(2i – 2,2) ? n/P? ;

odpar

for i = 1 to P dopar

/* Setiap prosesor menggabungkan dua sublist X dan Y dan memasukkan hasilnya di Z secara serial */

if i < P

then

gabungkan sublist di X yang diawali di x_BX(i) dan sublist Y yang diawali di y_BY(i)hingga sebuah

elemen yang lebih besar dari atau sama dengan L(2i,1) dicapai dan setiap X dan Y dan

memasukkan hasilnya di Z diawali pada posisi BX(i) + BY(i) -1

else

gabungkan sublist dari X yang diawali di x_BX(P) dan sublist Y yang diawali di y_BY(P)hingga tidak

ada lagi elemen yang tersisa baik di X maupun di Y dan masukkan hasilnya ke dalam Z yang

diawali pada posisi BX(P) + BY(P) -1

odpar

Paralel Algorithm Merging & Sorting, Parallel Algorithm

Variabel Acak Geometri (Geometric Random Variables)

1 November 2010 toosa Leave a comment

Misalkan ada suatu percobaan yang independent . Setiap kali percobaan itu akan memiliki kemungkinan sukses (probabilitas) sebesar p.

Jika X mewakili banyaknya percobaan awal sebelum akhirnya sebuah sukses terjadi, maka :

$P\left \{ X=n \right \} = p(1-p)^{n-1}, \; n\geq 1$

Sebenarnya rumus di atas dapat mudah dipahami bahwa untuk mendapatkan sukses yang ke-n maka pastilah (n-1) percobaan sebelumnya adalah gagal. Rumus ini berlaku dengan syarat setiap percobaan terjadi secara independent. (percobaan sebelumnya tidak mempengaruhi percobaan berikutnya).

Sebuah Variabel Acak yang memiliki probability mass function seperti di atas disebut Variabel Acak Geometri dengan parameter p.

Mean dari variabel acak geometri ini diperoleh dengan cara sebagai berikut :

$E\left [ X \right ]=\sum_{n-1 }^{\infty} np(1-p)^{n-1}=\frac{1}{p}$