April 2013 – OpenStat

Shuffle-Exchange Networks

30 April 2013 toosa Leave a comment

M.J.Quin pp.59-60

Jaringan Shuffle-Exchange mengandung n = 2^kbuah node yang ditandai dengan angka 0, 1, … , n-1, dan dua macam koneksi yang disebut shuffle dan exchange. Exchange menghubungkan sepasang nodes yang angkanya berbeda di bit yang terakhirnya. Koneksi?perfect shuffle menghubungkan node i dengan node 2i modulo (n-1), kecuali untuk node yang ke n-1,?dia terhubung dengan dirinya sendiri. Perhatikan gambar 3-8 berikut :

Gambar 3-8

Ini adalah gambar jaringan shuffle-exchange dengan 8 (delapan) buah nodes. Koneksi Shuffle ditandai dengan tanda panah bergaris penuh dan jalur exchange (pertukaran) ditandai dengan panah bergaris putus-putus.

Turunan dari shuffle-exchange salah satunya adalah perfect shuffle. Untuk mendapatkan pemahamam tentang perfect shuffle mari perhatikan ilustrasi berikut ini. Misalkan ada pengocokan kartu sejumlah 8 buah kartu. Mereka ditandai dengan angka 0,1,2,3,4,5,6,7. Jika tumpukan kartu tadi dibagi rata menjadi dua dan kemudian di kocok dengan sempurna, maka hasilnya adalah sebagai berikut : 0,4,1,5,2,6,3,7. Dengan memperhatikan gambar 3-8 di atas, posisi terakhir dari kartu yang dimulai dengan index i dapat ditentukan dengan mengikuti sambungan shuffle dari node i.

Misalkan $\inline a_{k-1}a_{k-2},\cdots , a_{1},a_{0}$ adalah alamat sebuah node di sebuah jaringan perfect-shuffle dalam bentuk biner. Sebuah data pada alamat ini akan berada di alamat? $\inline a_{k-2},\cdots , a_{1},a_{0},a_{k-1}$ sesuai dengan operasi?shuffle. Dengan perkataan lain, perubahan pada alamat dari sebuah data setelah operasi shuffle berkaitan dengan rotasi perputaran kiri (left cylic rotation) dari alamatnya sejauh 1 (satu) bit. Jika n = 2^k, maka k kali operasi shuffle memindahkan suatu data kembali ke lokasi asalnya.

The nodes through which a data item beginning at addressÂ i travels in response to a sequence of shuffles are called the necklaceÂ of i. No necklaceÂ is longer thanÂ k and aÂ necklace shorter thanÂ k is called aÂ short necklace. Figure 3-9 illustrateÂ the necklaces of the perfect shuffle network with eight nodes.

Gambar 3-9

Paralel Algorithm Perfect Shuffle, shuffle-exchange

Bitonic Merge

23 April 2013 toosa Leave a comment

Algoritma ini menjadi dasar untuk algoritma-algoritma sorting dengan waktu proses poli-logaritmik pada beberapa model komputasi paralel. Operasi dasarnya adalah Compare-Exchange: dua buah angka diarahkan masuk ke sebuah Comparator, di dalam comparator ini kedua nilai jika diperlukan akan dipertukarkan, sehingga akan berada pada urutan yang dikehendaki

Definisi 10.1 Bitonic Sequence adalah sederetan nilai $ a_{0}, \cdots ,a_{n-1}$ dengan sifat bahwa

ada sebuah index i , dimana $ 0\leq i\leq n-1$, sedemikian sehingga a₀ menaik secara monoton ke a_idan a_imenurun secara monoton hingga a_n-1, atau
ada sebuah pergeseran index yang berputar (cyclic shift) sehingga kondisi yang pertama terpenuhi

Coba Anda perhatikan sebuah grafik barisan bitonic di bawah ini, dia akan memiliki paling banyak ‘satu puncak’ dan ‘satu lembah’. Jangan lupa bahwa barisan ini ‘memutar’ dari elemen yang terakhir kembali ke elemen yang pertama.

10-5

Sebuah langkah compare-exchange bisa memecah sebuah barisan bitonic tunggal menjadi 2 (dua) buah barisan bitonic, sebagaimana disebutkan dalam Lemma 10.1 berikut ini :

Lemma 10.1 Jika n adalah genap, maka n/2 buah comparator cukup untuk mentransformasikan sebuah barisan bitonic dengan n buah nilai, $ a_0, a_1, a_2, \cdots , a_{n-2},a_{n-1}$ menjadi 2 (dua) buah barisan bitonic dengan n/2 buah nilai,

$ min(a_0,a_{n/2}), min(a_1,a_{n/2+1}),\cdots ,min(a_{n/2-1},a_{n-1})$
dan
$ max(a_0,a_{n/2}), max(a_1,a_{n/2+1}),\cdots ,max(a_{n/2-1},a_{n-1})$

Sedemikian sehingga tidak ada nilai yang terletak pada barisan yang pertama adalah lebih besar dari nilai yang terletak pada barisan yang kedua.

Anggaplah kita memiliki sebuah barisan bitonic, sebuah langkah compare-exchange membagi barisan ini menjadi dua buah barisan bitonic yang sama panjang yaitu n/2 . Dengan melakukan langkah ini secara rekursif akan menghasilkan barisan yang terurut.

10-8

Atau dengan kata lain, jika diberikan sebuah barisan bitonic dengan panjang n = 2^k , dimana k > 0, maka k buah langkah compare-exchange cukup untuk menghasilkan barisan yang terurut

Berikut ini adalah contoh mengurutkan barisan dengan panjang 16 yang di jalankan dalam 4 (empat) langkah compare-exchange.

10-10

10-12

Paralel Algorithm Bitonic Merge, Merging & Sorting

Bitonic Merge pada Shuffle-Exchange Nework

23 April 2013 toosa Leave a comment

Teorema 10.6. Sebuah daftar dengan n = 2^k buah elemen yang tidak terurut dan dapat diurutkan dalam waktu $\inline \Theta (log^{2}n)$ dengan jaringan $\inline 2^{k-1}[k(k-1)+1]$ komparator menggunakan skema interkoneksi shuffle-exchange secara exclusive (Stone, 1971)

Stone menyadari bahwa Pengurut Bitonic milik Batcher ini selalu membandingkan elemen-elemen dengan index yang berbeda tepat 1 bit pada bentuk biner nya. Dengan perfect shuffle, akan memperjalankan elemen pada posisi i ke posisi yang ditemukan., dengan memutar tampilan biner dari i satu bit ke kiri. Dengan demikian dua buah index yang tampilan biner nya berbeda tepat 1 bit dapat diperjalankan ke komparator yang sama dengan cara melakukan sejumlah shuffle tertentu.

Gambar berikut ini menunjukkan bagaimana bitonic merge dapat diimplementasi dengan menggunakan skema interkoneksi shuffle-exchange secara ekslusif.

Gambar 10-13

Sangat berbeda dengan Gambar 10-10, dimana interkoneksi antar komparator nya bervariasi dari tahap ke tahap lainnya. Keseluruhan proses pengurutan dapat diselesaikan dengan menggunakan interkoneksi shuffle-exchange. Kedua algoritma membutuhkan k bitonic merge untuk mengurutkan 2^k elemen, tetapi ketika merge ke-i di algoritma Batcher membutuhkan i langkah untuk total k(k+1)/2,

Algoritma

‘

Paralel Algorithm Bitonic Merge, Merging & Sorting, Perfect Shuffle

Memasang Eclipse di Ubuntu

13 April 2013 toosa Leave a comment

Cara memasang Eclipse di Ubuntu (Saya menggunakan Ubuntu 12.10) pada prinsip nya sangat mudah, sama dengan aplikasi-aplikasi lainnya di Ubuntu, caranya : Aktifkan Ubuntu Software Center, lalu pilih Eclipse dan Install. DONE !

Hanya saja versi Eclipse terakhir yang tersedia di repository Ubuntu 12.10 adalah eclipse-platform 3.8.0~rc4-1ubuntu1. Sehingga jika Anda ingin mendapatkan versi terakhir yaitu Juno 4.2.2 SR2, Anda perlu sedikit usaha dengan mendownload dari http://www.eclipse.org/downloads/ lalu pilih yang sesuai dengan platform (OS) yang Anda gunakan.

Saya sarankan kita mulai dari Eclipse yang paling standard yaitu Eclipse Classic 4.2.2, 182 MB. Berhubung file nya cukup besar, jangan lupa siapkan kopi dan snack untuk menikmati penantian downloading nya 🙂

Anda akan mendapatkan file eclipse-SDK-4.2.2-linux-gtk.tar.gz , kemudian extract dengan extract tools yang Anda sukai. Kalau saya lebih memilih menggunakan Nautilus yaitu sebuah File Manager standard dari Gnome yang default terpasang di Ubuntu. Caranya praktis, tinggal klik-kanan, lalu Extract Here, selesai ! 🙂

Tidak ada proses instalasi, tetapi dengan catatan bahwa Java sudah terinstall dengan baik di Ubuntu Anda. Saat tulisan ini dibuat saya menggunakan OpenJDK Java 7 Runtime.

Hasil extract eclipse-SDK-4.2.2-linux-gtk.tar.gz akan menghasilkan sebuah folder Eclipse. Masuklah ke dalamnya lalu jalankan file eclipse yang merupakan executable file. Done !Selanjutkan Anda akan diminta menentukan direktory kerja (workspace) nya ada dimana.

Jika ingin lebih mudah dan nyaman dalam mengaktifkan eclipse, silahkan buat Link di menu, atau diletakkan di Desktop.

Mudah bukan 🙂 Selamat menggunakan eclipse.

Software Development IDE

Ood-even Transposition Sort Algorithm

9 April 2013 toosa Leave a comment

Paralel Algorithm Sort

Enumeration Sort

9 April 2013 toosa Leave a comment

Asumsikan kita mempunyai Tabel dengan n buah elemen yang ditandai dengan $a_0,a_1,…,a_{n-1}$

Paralel Algorithm Sort

Menggabungkan Dua Daftar Terurut

8 April 2013 toosa Leave a comment

Sebuah Algoritma RAM yang optimal akan membuat satu elemen dalam satu waktu. Algoritma ini memerlukan paling banyak n – 1 buah perbandingan untuk menggabungkan 2 (dua) buah Daftar Terurut yang berukuran n/2. Kompleksitas waktunya $\inline \Theta (n)$ . Sedangkan algoritma PRAM hanya membutuhkan $\inline \Theta (log \: n)$ dengan sebuah prosesor untuk setiap elemennya. Dua daftar yang sudah terurut yang akan digabungkan ini memiliki elemen-elemen yang saling disjoint.

(Merging Two Sorted List – Quinn)

Paralel Algorithm Merging, Sorted List

Algoritma Paralel Pewarnaan Graph (Graph Coloring)

8 April 2013 toosa Leave a comment

Persoalan pewarnaan Graph (Graph Coloring) adalah mencari banyaknya warna yang dapat digunakan untuk mewarnai setiap vertex yang ada pada sebuah Graph sehingga tidak ada vertex yang bertetangga memiliki warna yang sama.

Asumsikan bahwa kita memiliki sebuah Graph dengan n buah vertex. Kemudian kita membuat sebuah matriks tetangga (matrik adjacency) n x n dan sebuah bilangan konstan c , sebuah prosessor disiapkan untuk setiap kemungkinan pewarnaan Graph. Contoh, prosesor $P(i_0,i_1, … , i_{n-1})$ berkaitan dengan pewarnaan vertex 0 dengan warna $i_0$, pewarnaan vertex 1 dengan warna $i_1$, … pewarnaan vertex n-1 dengan warna $i_{n-1}$

Setiap prosesor pada awalnya mengatur nilainya dalam candidate array berdimensi-n ke nilai 1 (satu). Kemudian menghabiskan waktu $\Theta (n^{2})$ untuk menentukan apakah untuk pewarnaan pada vertex tertentu dapat dilakukan, dua vertex yang bertetangga telah diberi warna yang sama. Jika A[j,k] = 1 dan $i_j = i_k$, maka proses pewarnaan salah, karena A[j,k] = 1 berarti vertex j dan k bertetangga, dan $i_j = i_k$ artinya j dan k memiliki warna yang sama. Jika prosesor mendeteksi pewarnaan yang salah ini, dia akan mengubah nilainya di candidate array menjadi 0. Setelah $n^2$ kali pembandingan, jika ada elemen di candidate array yang masih bernilai 1, maka pewarnaan dinyatakan benar. Dengan menjumlahkan semua elemen $c^n$ dalam candidate array, maka kita dapat menyatakan apakah proses pewarnaan dapat dilakukan (lihat gambar dan algoritma di bawah ini)

Kompleksitas : $\Theta (n^2)$ dengan menggunakan n buah Prosesor.

Paralel Algorithm coloring, Graph

Preorder Tree Traversal

2 April 2013 toosa Leave a comment

Preorder Traversal adalah proses kunjungan pada graph pohon dimana penandaan kunjungan dilakukan di awal yaitu ketika node untuk pertama kali terkunjungi. Urutan kunjungan mengikuti kaidah depth first search order. Secara sekilas persoalan preorder traversal seperti persoalan sekuensial. Coba perhatikan fungsi rekursif di bawah ini :

Dimana parallelisme nya ? Kita akan melihat bahwa cara pandang dengan vertex sebagai fokusnya akan menyebabkan kita melihat persoalan ini sebagai persoalan sekuensial murni yang tidak ada proses paralel nya.

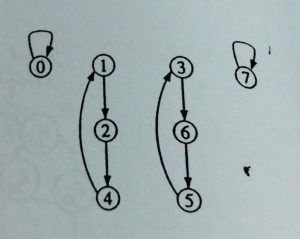
Sekarang, mari kita lihat dengan cara pandang yang berbeda. Mari kita pandang ruas/edge dari graph ini. Kita melihat bahwa ketika perjalanan kunjungan graph dilakukan, maka setiap ruas/edge akan dilewati 2 (dua) kali dengan arah yang berlawanan, turun dan naik. Jika kita pisahkan setiap ruas/edge ini menjadi 2, yang pertama menjadi ruas turun, dan yang satu lagi menjadi ruas naik, maka sekarang kita akan melihat persoalan preorder traversal ini menjadi sebuah persoalan singly-linked list.

Cara pandang terhadap ruas/edge inilah yang menjadikannya sebagai persoalan yang dapat diparalelkan dengan sebuah algoritma yang cepat. (dipublikasikan oleh Tarjan dan Vishkin 1984).

Selanjutnya mari kita bahas algoritma ini dengan lebih rinci. Algoritma ini memiliki 4 fase. Pada fase pertama, algoritma akan membentuk sebuah singly-linked list. Setiap vertex/simpul dari singly-linked list ini akan berkait dengan ruas penelusuran naik atau ruas penelusuran turun di dalam tree.

Pada fase kedua, algoritma akan memberikan bobot kepada semua vertex/node dari singly-linked list yang baru dibuat tersebut. Pada algoritma preorder traversal, sebuah vertex/node diberi label/tanda segera saat dilewati traversal/penelusuran edge yang turun. (Vertex root adalah pengecualian dan harus ditangani secara khusus). Untuk itu pada setiap vertex/node yang terkait dengan penelusuran edge turun diberi bobot 1 (satu)., artinya hitungan node nya bertambah ketika ruas/edge nya ditelusuri. Kemudian daftarkan element-element yang terakit dengan ruas/edge naik dengan bobot 0 (nol), karenanya hitungan node nya tidak akan bertambah ketika penelusuran pohon melaluinya saat menuju node yang sudah diberi label/tanda sebelumnya.

Pada fase ketiga kita menghitung rank dari daftar element untuk setiap elemen di sinly-linked list.

Langkah/fase keempat, prosesor2 yang memegang ruas turun menggunakan rank yang sudah dihitung olehnya untuk memberikan angka penelusuran/traversal preorder pada node-2 yang terkait dengannya (node di akhir ruas turun)

Implementasi alogritma ini menggunakan sturktur data yang tidak biasa dalam menampilkan pohon/tree nya.

Untuk setiap tree node, struktur data menyimpan : parent dari node, sibling langsung yang berada di kanannya (immediate sibling to the right) dan anak paling kiri (leftmost child).

Algoritma di bawah ini adalah algoritma PRAM untuk preorder tree traversal. Algoritma ini memasangkan setiap prosesor dengan setiap ruas/edge yang ditelusuri. Sebuah pohon/tree dengan n buan node akan memiliki n-1 buah ruas/edge. Karena kita membagi setiap ruas/edge menjadi ruas turun dan ruas naik , maka algoritma ini membutuhkan 2(n-1) buah prosesor untuk menghitung 2(n-1) elemen dari singly-linked list.

Setelah semua prosesor dalam keadaan aktif, mereka akan segera membentuk linked list yang terkait dengan preorder traversal. Diberikan ruas/edge (i,j), setiap prosesor harus menghitung penerusnya/successor dari ruas/edge tersebut dalam penelusurannya. Jika parent[i]=j, ruasnya akan menuju kebagian atas dari pohon, dari node anak ke parent nya. Ruas naik memiliki tiga macam successor. Jika anak memiliki sebuah sibling ruas successor akan bergerak dari parent node menuju ke sibling nya, selain itu jika anak memiliki kakek/grandparent , maka ruas successor akan bergerak dari node parent ke node kakek/grandparent nya. Jika kedua kondisi tersebut tidak terpenuhi maka artinya ruas berada di akhir/ujung dari pohon traversal, jadi selanjutnya kita letakkan sebuah loop di ujung dari daftar elemen ini. Dalam kasus ini kita juga mengetahui identitas dari node root/akar, dan kita jadikan nomor preordernya menjadi 0.

Berikutnya kita perhatikan kasus $parent[i] \neq j$ ; dimana ruas bergerak turun di dalam pohon, dari node parent ke anaknya. Hanya ada dua macam successor edge. Jika node anaknya memiliki anak, maka successor nya adalah edge dari anak ke cucunya. Selain itu, node anak adalah daun dan successor adalah ruas dari anak menuju parent nya.

Setelah prosesor membentuk linked list, mereka akan memberikan nilai posisi 1 untuk elemen yang merupakan ruas turun dan 0 untuk elemen yang merupakan ruas naik.

Nilai akhir dari nilai posisi ini menunjukkan angka penelusuran preorder antara daftar elemen ke ujung dari list. Untuk menghitung lebel dari setiap node preorder traversal, setiap prosesor dihubungkan dengan ruas turun dan dikurangangi nilai position nya dari n+ 1. Penamahan 1 karena penomoran preorder traversal dimulai dari 1 bukan 0

Paralel Algorithm PRAM, Preorder, Tree Traversal