M.J.Quin pp.59-60

Jaringan Shuffle-Exchange mengandung n = 2^k buah node yang ditandai dengan angka 0, 1, … , n-1, dan dua macam koneksi yang disebut shuffle dan exchange. Exchange menghubungkan sepasang nodes yang angkanya berbeda di bit yang terakhirnya. Koneksi?perfect shuffle menghubungkan node i dengan node 2i modulo (n-1), kecuali untuk node yang ke n-1,?dia terhubung dengan dirinya sendiri. Perhatikan gambar 3-8 berikut :

Gambar 3-8

Ini adalah gambar jaringan shuffle-exchange dengan 8 (delapan) buah nodes. Koneksi Shuffle ditandai dengan tanda panah bergaris penuh dan jalur exchange (pertukaran) ditandai dengan panah bergaris putus-putus.

Turunan dari shuffle-exchange salah satunya adalah perfect shuffle. Untuk mendapatkan pemahamam tentang perfect shuffle mari perhatikan ilustrasi berikut ini. Misalkan ada pengocokan kartu sejumlah 8 buah kartu. Mereka ditandai dengan angka 0,1,2,3,4,5,6,7. Jika tumpukan kartu tadi dibagi rata menjadi dua dan kemudian di kocok dengan sempurna, maka hasilnya adalah sebagai berikut : 0,4,1,5,2,6,3,7. Dengan memperhatikan gambar 3-8 di atas, posisi terakhir dari kartu yang dimulai dengan index i dapat ditentukan dengan mengikuti sambungan shuffle dari node i.

Misalkan adalah alamat sebuah node di sebuah jaringan perfect-shuffle dalam bentuk biner. Sebuah data pada alamat ini akan berada di alamat? sesuai dengan operasi?shuffle. Dengan perkataan lain, perubahan pada alamat dari sebuah data setelah operasi shuffle berkaitan dengan rotasi perputaran kiri (left cylic rotation) dari alamatnya sejauh 1 (satu) bit. Jika n = 2^k, maka k kali operasi shuffle memindahkan suatu data kembali ke lokasi asalnya.

The nodes through which a data item beginning at address i travels in response to a sequence of shuffles are called the necklace of i. No necklace  is longer than k and a necklace shorter than k is called a short necklace. Figure 3-9 illustrate  the necklaces of the perfect shuffle network with eight nodes.

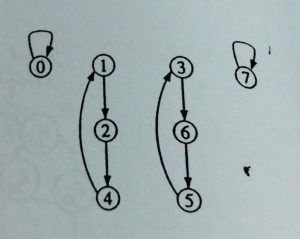
Gambar 3-9