Misalkan g(x) adalah sebuah fungsi. Kita ingin menghitung \( \theta \) yaitu :
&space;dx)
Apa yang menjadi dasar bahwa integral di atas dapat dihitung dengan menggunakan bilangan random \( \theta \)
Penjelasan :
Ambil U suatu bilangan acak yang terdistribusi secara uniform dan independent di interval (0,1).
Kemudian misalnya kita nyatakan \( \theta \) sebagai :
![\theta = E[g(U)]](http://latex.codecogs.com/gif.latex?\theta&space;=&space;E[g(U)])
Jika \(U_{1}, … , U_{k}\) adalah variabel random yang independent dan uniform di interval (0,1), maka menjadikan juga \(g( u_{i} )\) adalah sebagai variabel random yang independent dan terdistribusi secara identik dengan mean \( \theta \). Karena itu, dengan menggunakan dasar hukum kuat dari bilangan besar (the strong law of large numbers), mengikuti ketentuannya dengan probabilitas 1.
\(\large \sum_{i=1}^{k}\frac{g(U_{i})}{k} \to E[g(U)]= \theta \;\;\;\; ketika \; k \to \infty\)
Karena itu kita dapat mendekati \( \theta \) dengan cara membangkitkan sebanyak mungkin bilangan random \( u_{i}\) dan mengambilnya sebagai pendekatan kita terhadap nilai rata-rata (average) dari \(g( u_{i} ) \). Pendekatan semacam ini sering disebut sebagai pendekatan Monte Carlo.
Berikut ini adalah contoh algoritma dari bahasa BASIC yang dapat digunakan untuk mendekati nilai \( \theta \) :
10 RANDOMIZE
20 INPUT K
30 S = 0
40 FOR I = 1 TO k
50 U = RND
60 S = S + g(U)
70 NEXT
80 PRINT S/K
Nilai yang dihasilkan dari alogoritma ini adalah nilai dari \( \theta = \int_{0}^{1} g(x) dx \).
Kasus 1 :
Jika kita ingin menghitung :
\( \theta = \int_{a}^{b} g(x) dx \)
maka kita menggunakan substitusi \( y = (x-a)/(b – a), dy = dx / (b-a) \), sehingga :
![\begin{align*} \theta &= \int_{0}^{1} g(a+[b-a]y)(b-a)) dy\\ &= \int_{0}^{1} h(y) dy \end{align*}](http://latex.codecogs.com/gif.latex?\begin{align*} \theta &= \int_{0}^{1} g(a+[b-a]y)(b-a)) dy\\ &= \int_{0}^{1} h(y) dy \end{align*})
dimana h(y) = (b – a) g(a + [b – a] y ).
Dengan demikian kita dapat mendekati nilai \( \theta \) dengan membangkitkan bilang random secara kontinyu dan mengambil nilai rata-rata (average) dari h yang dihitung pada bilangan-bilangan random tadi.
Kasus 2 :
Jika kita ingin menghitung :
 dx)
kita bisa menggunakan substitusi 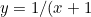, dy = - dx/(x + 1)^2 = -y^{2} dx)
Substitusi ini menggambarkan bahwa
- ketika \( x \to 0\) maka \( y \to 0\)
- ketika \( x \to \infty \) maka \( y \to 1\)
Catatan : ingat sifat integral tertentu :
 dx = - \int_{b}^{a} f(x) dx)
selanjutnya karena : 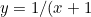)
 \\ &= - \frac{dx}{(x+1)^2}\\ &= - (\frac{1}{x+1})^2 dx\\ &= - y^2 dx\\ dx &= - \frac{1}{y^2} dy \end{align*})
kemudian
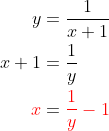
sehingga didapatkan identitas :
 dy)
dimana
=\frac{g(\frac{1}{y}-1)}{y^{2}})
